Web Client
This example shows you how to make a HTTP request using an Ethernet shield. It returns a Google search for the term "Arduino". The results of this search are viewable as HTML in the Serial Monitor.
Hardware Required
Arduino Board
Circuit
The Ethernet shield allows you to connect a WIZNet Ethernet controller to the Arduino boards via the SPI bus. It uses the ICSP header pins and pin 10 as chip select for the SPI connection to the Ethernet controller chip. Later models of the Ethernet shield also have an SD Card on board. Digital pin 4 is used to control the slave select pin on the SD card.
The shield should be connected to a network with an Ethernet cable. You will need to change the network settings in the program to correspond to your network.
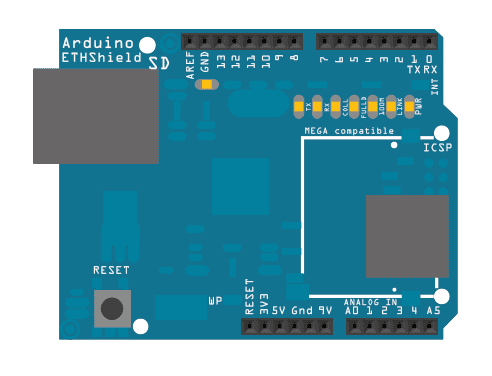
Image developed using Fritzing. For more circuit examples, see the Fritzing project page
In the above image, the Arduino board would be stacked below the Ethernet shield.
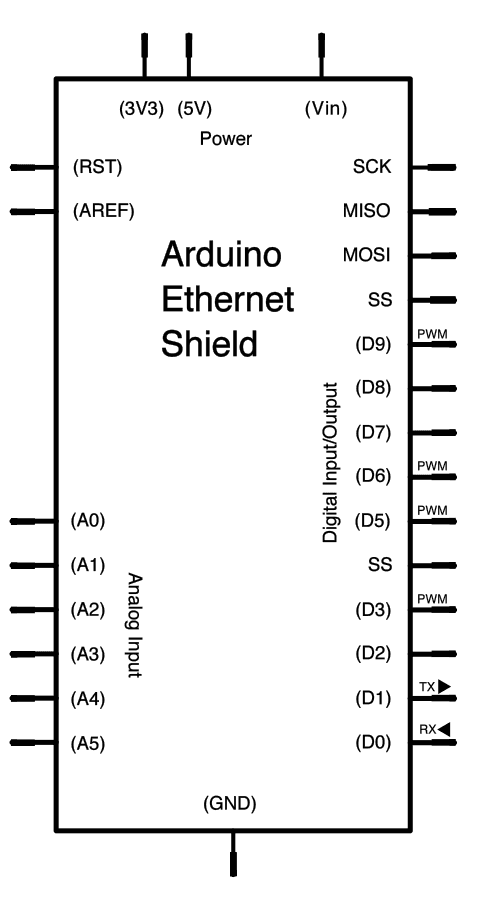
Schematic
Code
See also
Arduino Ethernet Shield - Product description.
Getting started with the Ethernet Shield - Get everything set up in minutes.
Ethernet library - Your reference for the Ethernet Library.
ChatServer - A simple server that distributes any incoming messages to all connected clients.
WebClientRepeating - How to make repeated HTTP requests using the Ethernet shield.
WebServer - A simple web server that shows the value of the analog input.
DhcpAddressPrinter - Get a DHCP address and print it on serial monitor.
DhcpChatServer - Connect to a Telnet server and print on serial monitor all the received messages; uses DHCP.
TelnetClient - Connect to a Telnet server and print on serial monitor all the received messages
BarometricPressureWebServer - Post data read from a pressure sensor using SPI.
UDPSendReceiveString - Send and receive text strings via the UDP protocol (Universal Datagram Packet).
UdpNtpClient - query a Network Time Protocol (NTP) server and get the information through serial monitor.
Last revision 2018/09/07 by SM